P-value কী এবং বৈজ্ঞানিক পরীক্ষা নিরীক্ষায় এই মানের গুরুত্ব
সূচিপত্র
মুখবন্ধ
Henry Gee-এর নাম অনেকেই শুনে থাকবেন। তিনি একজন Blogger ও লেখক, কিন্তু তার সবথেকে বড় পরিচয় তিনি বিখ্যাত science journal ‘Nature’ -এর একজন বিশিষ্ট সম্পাদক। তিনি একটি লেখা লেখেন The Guardian পত্রিকায় ১৯শে সেপ্টেম্বর, ২০১৩ সালে। লেখাটির নাম “Science: the religion that must not be questioned”[1], অর্থাৎ “বিজ্ঞান: যে ধর্মকে প্রশ্ন করা চলে না”। এই লেখাটির এক জায়গায় উনি বলছেন,
If this all sounds rather rarefied, consider science at its most practical. As discussed in Dr McLain’s article and the comments subjacent, scientific experiments don’t end with a holy grail so much as an estimate of probability. For example, one might be able to accord a value to one’s conclusion not of “yes” or “no” but “P<0.05”, which means that the result has a less than one in 20 chance of being a fluke. That doesn’t mean it’s “right”.
One thing that never gets emphasized enough in science, or in schools, or anywhere else, is that no matter how fancy-schmancy your statistical technique, the output is always a probability level (a P-value), the “significance” of which is left for you to judge – based on nothing more concrete or substantive than a feeling, based on the imponderables of personal or shared experience. Statistics, and therefore science, can only advise on probability – they cannot determine The Truth. And Truth, with a capital T, is forever just beyond one’s grasp. [2]
কথাটা আংশিক সত্যি। পরিসংখ্যান বা statistics একটি গুরুত্বপূর্ণ বিষয়। পরিসংখ্যান বৈজ্ঞানিক পদ্ধতির সাথে অঙ্গাঙ্গিক ভাবে জড়িত। কিন্তু তবুও প্রবাবিলিটি এবং পরিসংখ্যান ঠিক কি ভাবে কাজ করে এবং এটি ঠিক কিভাবে বৈজ্ঞানিক পদ্ধতিতে ব্যবহৃত হয় তা নিয়ে সাধারণ মানুষের কাছে তো বটেই অনেক সময়ে বৈজ্ঞানিকদের মধ্যেও সংশয় দেখা যায়। এটাও সত্যি যে, বিজ্ঞানের একমাত্র কাজ চরম সত্য খুঁজে বের করা নয়। কিন্তু এখানে P-value সম্পর্কিত মন্তব্যটি করা হয়েছে তা নিতান্ত বিভ্রান্তকর। এটি একটি frequentist’s approach বললেও অত্যুক্তি হবে না। পরিসংখ্যান এভাবে কাজ করে না। Henry Gee এর এই বক্তব্য জন সাধারনের মধ্যে বিজ্ঞান ও পরিসংখ্যান বিষয়ে এক ভ্রান্ত ধারনার সুত্রপাত করে। আরও একটি বিভ্রান্তিকর বিষয় হোল, “Science and religion“ এই ভান্ত কল্পকাহিনীর প্রচার এবং তার জন্য বিজ্ঞানীদের দোষারোপ করা। অধিকাংশ বিজ্ঞানীই, তারা কি কাজ করছেন এবং তার সীমাবদ্ধতা সম্পর্কে পুরোপুরি সচেতন এবং অবহিত। এই কারণে বিভিন্ন research article-এ একটি ‘limitation’ নামের একটি section প্রায়শই চোখে পড়বে। অনেক ক্ষেত্রেই বিভিন্ন মিডিয়া সাধারণ মানুষের কাছে জনপ্রিয়তা অর্জনের জন্য, সবকিছু সাদা-কালো ভাষায় তুলে ধরতে চায় বা অতি সরলীকরণ করে ফেলে।
১লা অগাস্ট, ২০১২ তে বিবিসি তে একটি খবর প্রকাশিত হয়, “Higgs boson results from LHC ‘get even stronger'” [3] শিরনামে। সেখানে বলা হচ্ছে,
Now one Higgs-hunting team at the Large Hadron Collider report a “5.9 sigma” levels of certainty it exists.
এই ‘sigma level’ বলতে এক P-Value কে বোঝানো হয়েছে। ‘Five sigma‘ বলতে p-value বা probability-কে বোঝায় যার মান 3×10-7 বা প্রায় 3.5 million ভাগে এক ভাগ। এই P-Value যদি কোন সত্যকে উদ্ঘাটন নাই করে, তাহলে Higgs Boson সনাক্তকরন নিয়ে এতো মাতামাতি কেন? কেনই বা আরও বেশী Sigma Value সমন্বিত ফলাফল অর্জন করতে চাওয়ার আকাঙ্ক্ষা? তাহলে এখন দেখি এই P-Value বলতে আমরা সত্যিই কি বুঝি।
P-value কেন গুরুত্বপূর্ণ?
ধরা যাক একটি নতুন ওষুধ আবিষ্কার হয়েছে। ওষুধের নাম ‘Drug A’, আর এই ওষুধটি যে রোগের জন্য ব্যবহৃত হয়, তার জন্য আগে থেকেই আরেকটি ওষুধ ছিল তার নাম ‘Drug B’। আমাকে দেখতে হবে এই নতুন আবিষ্কৃত ঔষধটি পূর্বের ওষুধটির চেয়ে বেশি কার্যকরী কিনা। ধরা যাক, Drug A পরীক্ষা নিরীক্ষার বাকি সমস্ত ধাপ পার করে এখন মানুষের উপর প্রয়োগ করার ছাড়পত্র পেয়ে গেছে।
এই পরীক্ষাটি করার জন্য, আমি একজন রোগীকে ‘Drug A’ দেওয়া হোল, আর একজন রোগীকে দেওয়া হোল ‘Drug B’। এখন দেখা গেল প্রথম ব্যক্তি সুস্থ হয়েছেন কিন্তু দ্বিতীয় ব্যক্তি সুস্থ হননি। এই পরীক্ষা থেকে কি সিদ্ধান্তে আসা যায় যে নব্য আবিষ্কৃত ওষুধ টি পুরনো ওষুধের থেকে ভালো? উত্তরটা হলো, না। শুধুমাত্র একটি বা দুটি ব্যক্তির ক্ষেত্রে এই পরীক্ষা করে আমরা সঠিক সিদ্ধান্তে উপনীত হতে পারি না। পুরনো ওষুধটি বহু কারণে ব্যর্থ হতে পারে। হতে পারে দ্বিতীয় ব্যক্তি এমন কোন ওষুধ খাচ্ছিলেন, যে ওষুধের সাথে ‘Drug B’-এর কোন রকমের drug interaction হয়েছিল। হতে পারে, এই দ্বিতীয় ব্যাক্তি, যার ক্ষেত্রে ‘Drug B’ ব্যর্থ হয়েছে, তার কোন allergy আছে। অথবা তার দেহে এমন কোন উৎসেচক আছে যা ‘Drug B’-কে দ্রুত পরিপাক করে ফেলে। আবার এও হতে পারে, প্রথম ব্যক্তি যিনি Drug A নিয়েছিলেন তার ক্ষেত্রে ওষুধটি কাজ করেছিল কেবলমাত্র placebo effect-এর জন্য। এই ধরনের পরীক্ষা ক্ষেত্রে এরকম ঘটনা ঘটতে পারে। তার মানে এই ধরনের পরীক্ষা একাধিক ব্যক্তির উপরে প্রয়োগ করে দেখা উচিত।
এখন ধরা যাক দুইজন ব্যক্তি কে প্রথম ওষুধ (Drug A) এবং বাকি দুজন ব্যক্তিকে দ্বিতীয় ওষুধ (Drug B) প্রয়োগ করা হলো। দেখা গেল প্রথম গ্রুপে দুইজন ব্যক্তি ভালো হয়ে গেছেন, কিন্তু দ্বিতীয় গ্রুপে একজন ভালো হয়েছে কিন্তু আরেকজন ভালো হয়নি। এখন প্রশ্ন হল, এই দ্বিতীয় পরীক্ষা থেকে কি এই সিদ্ধান্তে আসা যায় যে প্রথম ওষুধটি দ্বিতীয় ওষুধের থেকে বেশি কার্যকরী? এক্ষেত্রেও উত্তরটি না। তার কারণ এমন হয়ে থাকতে পারে যে প্রথম গ্রুপের দুটি মানুষের ক্ষেত্রে প্রথম ওষুধটি কাজ করেছে শুধুমাত্র একটি Placebo effect-এর জন্য। হতে পারে দ্বিতীয় গ্রুপের যে ব্যক্তি সুস্থ হয়েছে তার ক্ষেত্রেও placebo effect কাজ করেছে। হতে পারে দ্বিতীয় ব্যক্তি যিনি সুস্থ হননি তার ক্ষেত্রে কোনো রকম drug interaction বা allergy ছিল। তাই সঠিক সিদ্ধান্তে উপনিত হতে হলে আরো অনেক বেশী মানুষের উপরে পরীক্ষা করে দেখা দরকার।
ধরা যাক পরবর্তী ধাপে অনেক মানুষের উপরে এই পরীক্ষা করা হোল এবং তার ফলাফল নিম্নরূপ:
| Drug A | Drug B | |
|---|---|---|
| সুস্থ হয়ে উঠেছেন | 10543 (99.2%) | 25 |
| সুস্থ হয়ে ওঠেনি | 85 | 15055(99.83%) |
| সামগ্রিক | 10628 | 15080 |
উপরোক্ত পরীক্ষা দেখে খুব সহজেই এই সিদ্ধান্তে আসা যায় যে Drug A, Drug B-এর থেকে বেশি কার্যকর। যাদের ক্ষেত্রে Drug A প্রয়োগ করা হয়েছে তাদের শতকরা 99.2 ভাগ সুস্থ হয়ে উঠেছেন, যেখানে দ্বিতীয় ওষুধটির সফলতার হার খুবই কম। এই ক্ষেত্রে placebo এবং allergy-র সম্ভাবনা থাকলেও, এত বেশী সংখ্যক মানুষের ক্ষেত্রে প্রয়োগ করা হয়েছে যে, এই পরীক্ষার ফলাফলের উপর সেই বিভিন্ন কারণগুলির প্রভাব থাকার সম্ভাবনা কম বলেই ধরে নেওয়া যায়।
এবার ধরা যাক, সময় এবং অর্থের অপ্রাচুর্যের কারণে এত বেশী সংখ্যক মানুষের উপরে পরীক্ষাটি করা গেল না। খুব সীমিত কিছু সংখ্যক মানুষের উপরে এই পরীক্ষা করে যে ফলাফল পাওয়া গেল, তা নিম্নরূপ:
| Drug A | Drug B | |
|---|---|---|
| সুস্থ হয়ে উঠেছেন | 75 (37.5%) | 45 (22.5%) |
| সুস্থ হয়ে ওঠেনি | 125 | 155 |
| সামগ্রিক | 200 | 200 |
যখন এই পরীক্ষাটি সীমিত সংখ্যক কিছু মানুষের উপরে প্রয়োগ করা হলো তখন দেখা গেল প্রথম ওষুধের ক্ষেত্রে সুস্থ হওয়ার হার 37.5%, যেখানে দ্বিতীয় ওষুধের ক্ষেত্রে সুস্থ হওয়ার হার 22.5%। এই বিষয়ে কোন সন্দেহ নেই যে দ্বিতীয় পরীক্ষাটিতেও প্রথম ওষুধ (Drug A) প্রয়োগ করার ফলে, দ্বিতীয় ওষুধের (Drug B) তুলনায় বেশি মানুষ সুস্থ হয়েছেন। কিন্তু এই পরীক্ষার ফলাফল এমন নয়, যেখানে খুব আত্মবিশ্বাস নিয়ে একথা বলা যায় যে দ্বিতীয় ওষুধের তুলনায় প্রথম ওষুধটি নিঃসন্দেহে বেশি কার্যকরী। তার প্রথম কারণ, প্রথম পরীক্ষাটিতে সুস্থ হয়ে উঠেছেন এবং সুস্থ হয়ে ওঠেন নি এমন রোগীর সংখ্যার মধ্যে একটি বিশাল ফারাক ছিল, কিন্তু দ্বিতীয় পরীক্ষায় এই তফাত খুব বেশী নয়। দ্বিতীয়তঃ দ্বিতীয় পরীক্ষাটিতে রোগীর সংখ্যা খুব বেশি নয়। যেহেতু আমরা জানি, যে কোনো পরীক্ষা-নিরীক্ষাতেই ভুল ভ্রান্তি হবার সম্ভাবনা থাকে এবং অসংখ্য অজানা প্রভাবক একটি পরীক্ষা কে প্রভাবিত করতে পারে, তাই জন্যে এটা নির্ণয় করা জরুরি যে একটি পরীক্ষার ফলাফল থেকে কতটা আত্মবিশ্বাসের সাথে আমরা সিধান্তে উপনীত হতে পারি। আর এখানেই P-Value-এর গুরুত্ব।
আরও একটি উদাহরন দেখা যাক। ধরা যাক একটি স্কুলে 100 জন ছাত্র পড়ে। কোন এক পরীক্ষায় তাদের গড় নম্বর 85, কিন্তু তাদের মধ্যে 30 জনকে randomly select করে দেখা গেল, এই randomly selected group-এর গড় নম্বর 95। এখান থেকে আমরা যে সিদ্ধান্তে উপনীত হতে পারি:
- এই ত্রিশটি ছাত্র আলাদা, অথবা
- অথবা এদের মধ্যে কোন পার্থক্য নেই যে পার্থক্য আমরা দেখছি তা কোন random chance-এর জন্য, যেহেতু এমন অনেক ছাত্র আছে যাদের নাম্বার 85 থেকে বেশি, আবার এমন ছাত্র আছে যাদের নম্বর 85 থেকে কম।
এখন আমরা কিভাবে জানবো কোন সিদ্ধান্তটি সঠিক। তার জন্য দুটি উপায় হতে পারে। হয় আরো বেশি সংখ্যক ছাত্র নিয়ে তাদের উপরে পরীক্ষা করা, অথবা আরেকটি নতুন পরীক্ষা করা যেখানে ক্ষেত্রে অন্য ছাত্র চয়ন করা, অথবা ‘Random chance probability’ নির্ণয় করা। অনেক সময় এমন হতে পারে যে আরও বেশিসংখ্যক ছাত্র নিয়ে এই পরীক্ষা করা সম্ভব নয়, অথবা শুধুমাত্র একবারই এই পরীক্ষাটি করা যাচ্ছে, কারণ এই পরীক্ষা করার পরে স্কুল ছুটি হয়ে গেছে। তখন আর ছাত্রদের পাওয়া যাবে না। তাহলে আমাদের প্রথম পরীক্ষাটির উপরই নির্ভর করতে হবে। তাহলে আমাদের কাছে তৃতীয় পথটিই খোলা থাকছে। যেহেতু এই পরীক্ষা করার সময় কোন নির্দিষ্ট নিয়ম মেনে ছাত্রদের চয়ন করা হয়নি, তাই প্রতিটা ছাত্রেরই সমান সম্ভাবনা ছিল এই পরীক্ষার অন্তর্ভুক্ত হওয়া, অর্থাৎ ব্যাপারটি ছিল। এমন হয়ে থাকতে পারে, কোনো কারণবশত শুধুমাত্র সেই ছাত্র গুলিই এই পরীক্ষার অন্তর্ভুক্ত রয়েছে যাদের গড় নম্বর বেশি। আমাদেরকে সেই সম্ভাবনায় এখানে নির্ণয় করতে হবে। আর সেখানেই P-Value এর গুরুত্ব।
অর্থাৎ মহাবিশ্বের সমস্ত তথ্য সংগ্রহ করে যেহেতু একটি পরীক্ষা করা সম্ভব নয়, তাই প্রায়শয়ই একটি সীমিত তথ্যের উপর আমাদের নির্ভর করতে হয়। যেমন, একটি টীকা আবিষ্কারের পর প্রতিটি মানুষের উপর প্রয়োগ করে তার ফলাফল নির্ণয় করা সম্ভব নয়। P-Value একটি নাম্বার যার মান ০ থেকে ১ পর্যন্ত হয়ে থাকে। আর এই মানটি নির্দেশ করে কি পরিমান আত্মবিশ্বাসের সাথে একটি পরীক্ষার ফলাফল আমরা গ্রহন করতে পারি। তার মানে, Drug A এবং Drug B নিয়ে আমরা যে পরীক্ষা করেছি, সেখানে এই নাম্বার আমাদের বলবে আমরা কতো আত্মবিশ্বাস নিয়ে আমরা এই কথা বলতে পারি যে এই দুটি ওষুধ আলাদা অথবা কোনটা বেশী কার্যকর। একদম প্রথমের পরীক্ষাটিতে যেখানে রোগীর সংখ্যা অনেক বেশী ছিল, সেখানে P-Value কম, আর দ্বিতীয় পরীক্ষাটিতে P-Value-র মান বেশী। অর্থাৎ P-Value এর মান ০ এর যত কাছাকাছি হবে, তত বেশী আত্মবিশ্বাসের সাথে আমরা বলতে পারবো যে ‘Drug-A’ তত বেশী কার্যকরী।
যেকোনো পরীক্ষার শুরুতেই সেই পরীক্ষার গুরুত্ব অনুযায়ী আমরা একটি threshold বা সীমা নির্ধারণ করে নিতে পারি, P-Value সেই সীমার নীচে থাকলে আমরা আত্মবিশ্বাসের সাথে একটি সিধান্তে উপনীত হতে পারি। প্রয়োজনে সেই পূর্ব নির্ধারিত সীমা কমিয়ে আনতে পারি, যাতে পরীক্ষালব্ধ ফলাফলের উপর আরও বেশী আত্মবিশ্বাস স্থাপন করা যায়।
এই সীমা নির্ধারণ করবো কিভাবে?
এখন প্রশ্ন হল একটি পরীক্ষায় আমরা এই সর্বোচ্চ সীমা নির্ধারণ করবো কিভাবে? প্রথম উদাহরণটি ধরা যাক। এই সীমা কত হলে আমরা খুব আত্মবিশ্বাসের সাথে এই কথা বলতে পারি যে প্রথম ওষুধ, দ্বিতীয় ওষুধের থেকে বেশি কার্যকর? অর্থাৎ P-Value কত হলে আমাদের এই পরীক্ষার ফলাফল যথেষ্ট আত্মবিশ্বাস প্রদান করবে? সাধারণত আমরা এই সর্বোচ্চ সীমা নির্ধারণ করি 0.05। এর অর্থ প্রথম এবং দ্বিতীয় ওষুধের মধ্যে সত্যিই যদি কোনো পার্থক্য না থাকে, এবং আমরা এই পরীক্ষাটি যদি বহুবার করি, হলে শতকরা 5 ভাগ ক্ষেত্রে ভুল সিদ্ধান্তে উপনীত হতে পারি। এর অর্থ এই যে, Drug A ও Drug B -এর মধ্যে কোন পার্থক্য না থাকা সত্ত্বেও আমরা শতকরা ৫ ভাগ ক্ষেত্রে এই ভুল সিধান্তে উপনীত হব যে এদের মধ্যে পার্থক্য আছে। আরও একটু বিস্তারিত ভাবে জানা যাক।
ধরা যাক এই নতুন আবিষ্কৃত ওষুধটি দুটি ভিন্ন গ্রুপের রোগীদের মধ্যে প্রয়োগ করা হল। এখন যেহেতু একই ওষুধ এই দুই গ্রুপের মধ্যে প্রয়োগ করা হয়েছে, তাই এই দু’টি গ্রুপের মধ্যে যে কোনো পার্থক্য পরিলক্ষিত হলে, ধরে নেয়া যেতে পারে কোন allergy, অথবা কোন placebo effect, অথবা কোন drug interaction, অথবা কোন metabolic পার্থক্য অথবা কোন অজানা কারণ এই বৈষম্যের জন্য দায়ী। নীচের বিবরণীটি লক্ষ্য করুন,
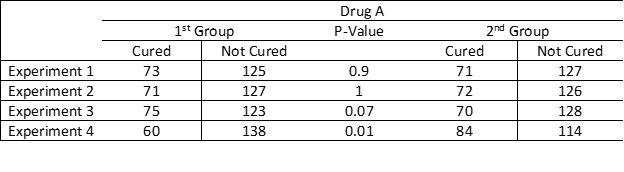
এখানে চারটি বিভিন্ন পরীক্ষার ফলাফল ও তার P-Value প্রকাশিত হয়েছে। প্রথম পরীক্ষাটিতে P-Value-র মান ০.৯, যা ০.০৫ এর থেকে অনেক বেশী। তাই আমরা বলতে পারি এই গ্রুপটিতে কোন পার্থক্য পরিলক্ষিত হচ্ছে না। এই পরীক্ষাটি বহুবার পুনরাবৃত্তি করা হোল। এবং দেখা গেল অধিকাংশ ক্ষেত্রেই P-Value র মান অনেক বেশী। কিন্তু চতুর্থ পরীক্ষাটি লক্ষ্য করুন। এখানে P-Value-র মান ০.০৫ এর অনেক কম। তার মানে এই পরীক্ষাটি দেখে মনে হোল যে এই দুটি গ্রুপের মধ্যে একটি পার্থক্য আছে।
বহুবার পরীক্ষা করতে করতে একবার দুবার এমনি হতেই পারে যে একটি গ্রুপে কোন কারণে এমন কিছু রোগীকেই বেশী চয়ন করা হয়ে যাদের এই ওষুধটির প্রতি কোন allergy আছে, আর দ্বিতীয় গ্রুপটিতে যারা আছেন তাদের ক্ষেত্রে কোন কারণে Placebo Effect বেশী কাজ করেছে। তাই, এক্ষেত্রে কোন পার্থক্য না থাকলেও ফলাফল দেখে মনে হচ্ছে যেন কোন পার্থক্য আছে। এই ধরনের ভ্রান্তিকে বলা হয়, False Positive, অর্থাৎ P-Value র ক্ষুদ্র মান এমন এক পরিস্থিতিতে যেখানে সত্যিই কোন পার্থক্য নেই।
P-Value-র সীমা ০.০৫ বেঁধে দেওয়ার অর্থ হোল, শতকরা ৫ ভাগ পরীক্ষার ক্ষেত্রে False Positive ফলাফল আসার সম্ভাবনা। অর্থাৎ প্রথম এবং দ্বিতীয় ওষুধের মধ্যে যদি সত্যিই যদি কোনো পার্থক্য না থাকে, তাহলে শতকরা 5 ভাগ পরীক্ষায় এমন একটি P-Value পাওয়া যাবে যার মান 0.05 এর কম (False Positive)। ওষুধটি যদি সত্যিই গুরুত্বপূর্ণ একটি একটি ওষুধ হয়, তাহলে আমরা আরো ক্ষুদ্র একটি সীমা নির্ধারণ করতে পারি। খুব ক্ষুদ্র একটি সীমা নির্ধারণ করলে, তাতে অনেক বেশি সময় এবং অর্থ অপচয় হতে পারে; যা হয়তো প্রয়োজনের অতিরিক্ত হয়ে দাঁড়াতে পারে। পরিসংখ্যান তত্ত্বে এইভাবে একটি সিদ্ধান্তে উপনীত হওয়ার প্রচেষ্টাকে বলা হয়, Hypothesis Testing বা ‘অনুমান পরীক্ষা’। প্রথমেই দুই ধরনের Hypothesis উপস্থাপন করা হয়। এদের মধ্যে একটি ‘Null Hypothesis’, অপরটি ‘Alternate Hypothesis’। উদাহরন হিসাবে ধরা যেতে পারে, Drug A এবং Drug B নিয়ে আমরা যে পরীক্ষাটি দেখেছিলাম, সেখানে Null Hypothesis হোল, “Drug A এবং Drug B এর মধ্যে কার্যকারিতার কোন পার্থক্য নেই”। এবং Alternate Hypothesis ঠিক তার উল্টো, অর্থাৎ Alternate Hypothesis বলছে এদের মধ্যে পার্থক্য আছে। P-Value এই Null Hypothesis কে প্রত্যাখান বা খারিজ করতে সাহায্য করে। অর্থাৎ যদি পরীক্ষালব্ধ P-Value পূর্বনির্ধারিত মানের কম হয় তাহলে আমরা Null Hypothesis-টি খারিজ করতে পারি।
আরও একটি গুরুত্বপূর্ণ বিষয় এখানে উল্লেখ করা উচিত যে, P-value যদিও দুটি ওষুধের মধ্যে পার্থক্য আছে কিনা নির্ধারণ করতে সাহায্য করে, কিন্তু সেই পারথক্যের মাত্রা নির্ধারণ করে না। নীচের উদাহরনটি দেখা যাক,

এখানে প্রথম পরীক্ষাটিতে সুস্থ হয়ে ওঠা রোগীদের পার্থক্য 8%, কিন্তু দ্বিতীয় পরীক্ষা দিতে সুস্থ হয়ে ওঠা রোগীদের পার্থক্য কেবল মাত্র 1%; কিন্তু প্রথম পরীক্ষাটিতে P-Value 0.24 কিন্তু দ্বিতীয় পরীক্ষাতে P-Value 0.04। অর্থাৎ প্রথম পরীক্ষা অপেক্ষা দ্বিতীয় পরীক্ষা থেকে অনেক বেশী আত্মবিশ্বাসের সাথে এই কথা বলা যায় যে প্রথম এবং দ্বিতীয় গ্রুপের মধ্যে পার্থক্য আছে। তাই sample size যত বেশী হবে Null Hypothesis টি তত বেশী আত্মবিশ্বাসের সাথে প্রত্যাখান করা যাবে।
সহজ কথায়, Null Hypothesis প্রত্যাখ্যান করার মত যথেষ্ট প্রমান আচে কিনা সেটা যাচাই করাই P-Value।
P-Value নির্ণয় করা হয় কিভাবে?
P-value মানে যে কেবল Probability নয়, তা এতক্ষণে পরিষ্কার হয়ে গেছে আশা করি। Probability এবং P-Value-র মধ্যে সম্পর্ক থাকলেও তারা এক নয়। একটা খুব সহজ উদাহরন দেখা যাক। ধরা যাক, একটি মুদ্রা আছে, যার একদিক Head(H) ও অপরদিকে Tail(T)। এই কয়েনটি যদি একটি সাধারণ Fair কয়েন হয় তাহলে, H ও T পড়ার সম্ভাবনা ৫০%। ধরা যাক, পর পর দুইবার এই কয়েনটি টস করা হবে। উভয় ক্ষেত্রেই H ও T পড়ার সম্ভাবনা ৫০%। এখন আমাদের নির্ণয় করতে হবে, পর পর দুই বার H পড়ার সম্ভাবনা কত? এবং পর পর দুইবার H পড়ার P-Value কত?
প্রথম প্রশ্নের উত্তর সহজ। চারটি সাম্ভাব্য ফলাফল, HH, HT, TH, TT; যাদের মধ্যে HH পড়ার সম্ভাবনা তাহলে 1/4=0.25। একই ভাবে পর পর দুই T পড়ার সম্ভাবনাও 0.25। একবার H ও একবার T পড়ার সম্ভাবনা 2/4=0.5।
এবার P-Value নির্ণয় করা যাক। কিন্তু তার আগে P-Value-র সংজ্ঞাটা আগে জেনে নেওয়া যাক।
A P-Value is the probability that random chance generated the data, or something else that is equal or rarer.
উপরোক্ত এই সংজ্ঞাটি থেকে আমরা P-Value নির্ণয়ের চেষ্টা করি। এই সংজ্ঞার তিনটি অংশ। প্রথম অংশটি হোল, “random chance generated the data”। আমরা জানি HH পড়ার সম্ভাবনা 0.25। দ্বিতীয় অংশ, “something else that is equal”। আমরা জানি, TT পড়ার সম্ভাবনা 0.25। তৃতীয় অংশ, “rarer”। কিন্তু আমাদের এই পরীক্ষায় HH বা TT পড়ার থেকে আর কোন দুর্লভ ফলাফল পাওয়া সম্ভব নয়, তাই এই অংশের মান শুন্য। তাই এই পরীক্ষায় P-Value, 0.25+0.25=0.5।
ধরা যাক, আরেকটি কয়েন নিয়ে টস করতে গিয়ে দেখা গেল, পর পর পাঁচবার H পড়েছে। এখন এই ফলাফল থেকে কত নিশ্চিয়তার সাথে বলা যায় যে কয়েনটি একটি Fair coin নয়। তাহলে প্রথমেই নির্ণয় করা যাক, পর পর পাঁচ বার H পড়ার সম্ভাবনা কত? উত্তর হোল, (1/2)5= 1/32। ঠিক একই ভাবে পর পর T পড়ার সম্ভাবনা 1/32। এবং এই দুই ধরনের ফলাফলা ছাড়া আর কোন দুর্লভ ফলাফল নেই। তাহলে P-Value হোল 1/32+1/32=0.0625।
ঠিক একই ভাবে ধরা যাক, পর পর ১০ বার H পড়েছে। তাহলে P value 2(1/2)10 = 0.001953125।
তাহলে দেখা গেল, কোন কয়েন ‘Fair’ কিনা সেই সিধান্তে উপনীত হতে হলে যত বেশী বার Toss করা হবে, ততই বেশী আত্মবিশ্বাসের সাথে একটি সিধান্তে উপনীত হওয়া যাবে।
আরও একটু পরিষ্কার ভাবে বোঝার জন্য, আর একটি উদাহরন দেখি। ধরা যাক, এবার আবার চারবার H ও একবার T পড়ার p-Value নির্ণয় করতে হবে। সেক্ষেত্রে, P-Value= Pr(4H and 1T)+ Pr(1H and 4T)+ Pr(5H) + Pr(5T)= 0.15625+0.15625+0.03125+0.03125=0.375।
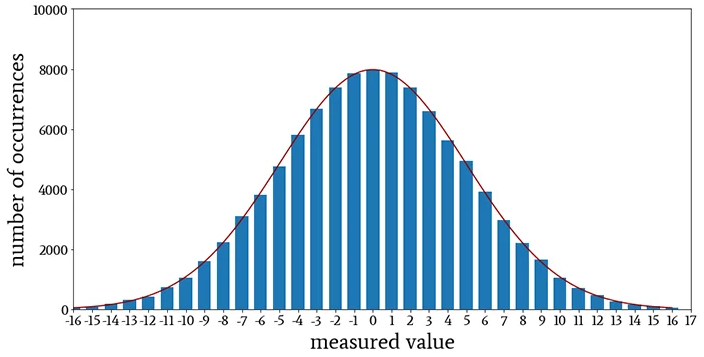
এবার আসা যাক কিছু বাস্তব উদাহরনে। ধর যাক, আমাদের কোন একটি জনগোষ্ঠীর Normal Hemoglobin level নির্ণয় করতে হবে। সাধারণভাবে দেখা যায় একটি Population এর মধ্যে এই Hemoglobin এর যা যা মান হতে পারে তা একটি normal distribution এর মধ্যে পড়ে। শুধু Hemoglobin নয়, আরও অনেক অনেক বৈশিষ্ট্য এইভাবে normal distribution এর মধ্যে পড়ে, যেমন উচ্চতা, ওজোন ইত্যাদি ইত্যাদি। নীচের ছবিদুটি দেখা যাক,


যদি কোন জনগোষ্ঠীর মধ্যে গড় Hemoglobin যদি 14.5 হয় এবং সমস্ত মানুষের Hemoglobin level যদি একটি normal distribution অনুযায়ী হয়, তাহলে mean থেকে +/-3SD বা Sigma value এর মধ্যে 99.7% value চলে আসবে। Mean value থেকে +/-2SD এর মধ্যে 95.4% value চলে আসবে।
CERN-এর 5 Sigma Value-র গুরুত্ব
Five sigma(σ) বলতে এমন একটি P-value-কে বোঝায় যার মান 3×10-7, অথবা 1 in 3.5 million। এর অর্থ এই নয় যে Higgs boson-র অস্ত্বিত্ব আছে না নেই তার সম্ভাবনা। এর অর্থ এই যে, যদি কণাটির অস্ত্বিত্ব না থাকে, তা হলেও CERN-এর বিজ্ঞানীরা যে তথ্য পেলেন, সেই তথ্য পাওয়ার সম্ভাবনা। তাই যতই সেই five sigma থেকে আরও বেশী significance level-এর দিকে যাওয়া যাবে, ততই বেশী নিশ্চিত হওয়া যাবে বিশ্বাসযোগ্যতা সম্পর্কে।
উপসংহার
বিজ্ঞান এমন একটি অধ্যয়ন ক্ষেত্র, যা স্বাভাবিক ভাবেই খুবই রক্ষণশীল। বিজ্ঞানীরা যে কোনও বিষয়েই নিশ্চিত, এই কথা বলতে অত্যন্ত দ্বিধাগ্রস্থ হন। প্রকৃতপক্ষে, বিজ্ঞানের একটি অলিখিত নিয়ম হ’ল, একজন বিজ্ঞানীকে এই সম্ভাবনা অবশ্যই মাথায় রাখতে হবে যে, পরবর্তী পরীক্ষা নিরীক্ষা থেকে এমন কোন অতিরিক্ত তথ্য উথে আসতে পারে, যা বর্তমান ধারনাকে নস্যাৎ করে দেবে। হতেই পারে, সেই পূর্ববর্তী ধারনা খুবই পছন্দের একটি ধারনা। এই অলিখিত নিয়মটি বিজ্ঞানী মাত্রেই অনুসরন করেন।
আমাদের আগের একটি উদাহরনের কথাই ধরা যাক। আমাদের কাছে একটি coin ছিল আর আমাদের নির্ধারণ করতে হত সেই coinটি একটি fair coin কি না। আমি এই coin নিয়ে চারবার toss করলাম আর প্রতিবারই দেখলাম আমার এই coinটি head পড়েছে। আমি এই পরীক্ষা থেকে একটা সন্দেহ প্রকাশ করতে পারি, কিন্তু একদম নিশ্চিতভাবে একথা বলতে পারি না যে, এই coinটি অবশ্যই fair coin নয়। কারণ পরবর্তী আরও ১০০বার toss করার পর হয়তো দেখা গেল, সমান সংখ্যক বার H এবং T পড়েছে।
আবার এমনও হতে পারে, পরবর্তী ২০ বার toss করায় দেখা গেলো যে, ১৯ বার H এবং ১ বার T এসেছে। তাহলে অনেক বেশী নিশ্চিত ভাবে আমরা বলতে পারি যে এই coinটি একটি ‘Fair coin’ না হবার সম্ভাবনা অনেক বেশী। কিন্তু পরবর্তী পরীক্ষা নিরীক্ষায় এমন তথ্য প্রমান উথে আসতেই পারে, যা এই পূর্ববর্তী ধারনা নস্যাৎ করে দিতে পারে, আর বিজ্ঞানীরা সেই সম্ভাবনাকে কখনই উড়িয়ে দেন না; আর এখানেই বিজ্ঞানের সৌন্দর্য। বিজ্ঞান ও বিজ্ঞানীরা এই দুই সম্ভাবনার প্রতি সমান উন্মুক্ত।
অন্য ভাবে বলতে গেলে, আমরা coinটি নিয়ে স্বল্প কয়েকবার toss করলাম, আর প্রতিবার H এলেও আমরা প্রাথমিক ভাবে ধারনা করতে পারি যে ‘fair coin’ নয়। কিন্তু আরও নিশ্চিত হবার জন্য, আরও তথ্য প্রমান প্রয়োজন। আর সেই কারণেই আমরা আরও অসংখ্য বার coin toss করলাম। সারাদিন ধরে coin toss করলাম। দেখা গেল H এর সংখ্যা T এর থেকে অনেক অনেক অনেক গুণ বেশী। একজন সাধারণ মানুষ হয়তো এখান থেকে হয়তো খুব দৃঢ়ভাবে এই সিধান্তে উপনীত হতে পারেন যে এটি একটি ‘Fair Coin’ নয়। কিন্তু একজন বিজ্ঞানীকে জিজ্ঞাসা করুন, তিনি বলবেন যে তিনি এই coin-টি ‘Fair Coin’ হবার সম্ভাবনা খুব খুব খুব কম। অথবা বলবেন তিনি 99.99999% নিশ্চিত যে এই কয়েন একটি ‘fair coin’ নয়। এই পার্থক্যের কারণ হোল, বিজ্ঞানীরা যা ধারনা করেন সেই ধারনার যথার্থতা কতোটা, তার মানও নির্দেশ করেন। কারণ তারা জানেন, প্রতিটি ‘event’ স্বতন্ত্র এবং পূর্বের ‘event’এর উপর নির্ভরশীল নয়, তাই যদিও ক্ষুদ্র এবং নগন্য, কিন্তু এক বিশাল সংখ্যকবার H আসা একেবারেই অসম্ভব নয়।
একজন সাধারণ মানুষ এই কথা বলতেই পারেন, “ও বুঝলাম! তাহলে এই ধারনা একদম সঠিক নয়?” কিন্তু একজন বিজ্ঞানী বলছেন যে, তিনি নিশ্চিত, কিন্তু তার এই ধারণা একটি যুক্তিযুক্ত সন্দেহের উর্ধে নয়।
তথ্যসূত্র
- https://www.theguardian.com/science/occams-corner/2013/sep/19/science-religion-not-be-questioned[↑]
- Henry Gee, (Thu 19 Sep 2013), Science: the religion that must not be questioned, Retrieved from https://www.theguardian.com/science/occams-corner/2013/sep/19/science-religion-not-be-questioned[↑]
- Higgs boson results from LHC ‘get even stronger’[↑]



p-value hacking সম্পর্কে কিছুই লিখলেন না, আশা করি লিখবেন। নয়তো এটা dishonesty হবে।